Propagation des ondes dans les métamatériaux et les milieux dispersifs

Ce thème concerne les milieux propagatifs dont les caractéristiques physiques, généralement représentées par des constantes positives, deviennent négatives dans certaines gammes de fréquences. Cela implique notamment que ces milieux sont dispersifs, au sens où leurs caractéristiques physiques dépendent de la fréquence.

Ces matériaux peuvent être naturels, comme les métaux et les plasmas où la permittivité diélectrique est presque réelle et négative dans une certaine gamme de fréquences. Ils peuvent être aussi artificiels, on parle alors de métamatériaux : c'est le cas des matériaux à indice négatif qui ont à la fois une permittivité diélectrique négative et une perméabilité magnétique négative à certaines fréquences, et des métamatériaux hyperboliques, qui sont des matériaux anisotropes, avec un tenseur de permittivité non positif.

Tous ces matériaux donnent lieu à des phénomènes inhabituels et les applications physiques possibles sont innombrables. En particulier, les matériaux à indice négatif font rêver les physiciens à des dispositifs spectaculaires comme la lentille parfaite ou la cape d'invisibilité.

L'analyse mathématique et numérique des modèles associés, tant dans le domaine temporel que dans le domaine fréquentiel, soulève de nombreuses questions ouvertes et de nouveaux défis. Depuis plus de deux décennies, POEMS a grandement contribué à la compréhension de ces questions et à l'élaboration de solutions adaptées : citons notamment l'approche de T-coercivité pour les problèmes de transmission à changement de signe et les Generalized Perfectly Matched Layers pour les matériaux à indice négatif.

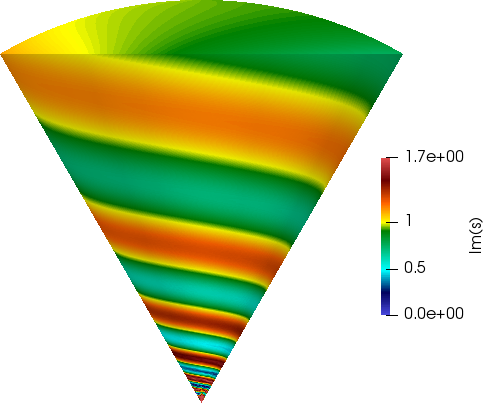
Une contribution importante de POEMS concerne l'effet des coins à la frontière d'un matériau négatif, qui donnent lieu à un phénomène de « trou noir » lié au comportement des plasmons de surface près des coins. Des études plus récentes concernent des matériaux anisotropes pour lesquels les valeurs propres du tenseur de permittivité diélectrique sont de signes opposés. Ces matériaux sont dits « hyperboliques », ce qui traduit le fait que la propagation des ondes harmoniques est décrite par un problème hyperbolique plutôt qu'elliptique, un exemple typique étant l'équation de Klein-Gordon.