Phénomènes couplés pour les ondes dans les fluides et les solides
Le laboratoire POEMS étudie la propagation acoustique dans des milieux complexes qui couplent des phénomènes se propageant à des vitesses très différentes. Un premier exemple est le cas d'un fluide en mouvement (aéroacoustique), dans lequel les ondes acoustiques et les ondes hydrodynamiques (la vorticité) se propagent à des vitesses très différentes. Un deuxième exemple est donné par un solide élastique, couplant naturellement des ondes de pression et de cisaillement, ce qui conduit dans le cas dégénéré d'un matériau quasiment incompressible à des vitesses très différentes des deux ondes.
Aéroacoustique via les équations de Goldstein
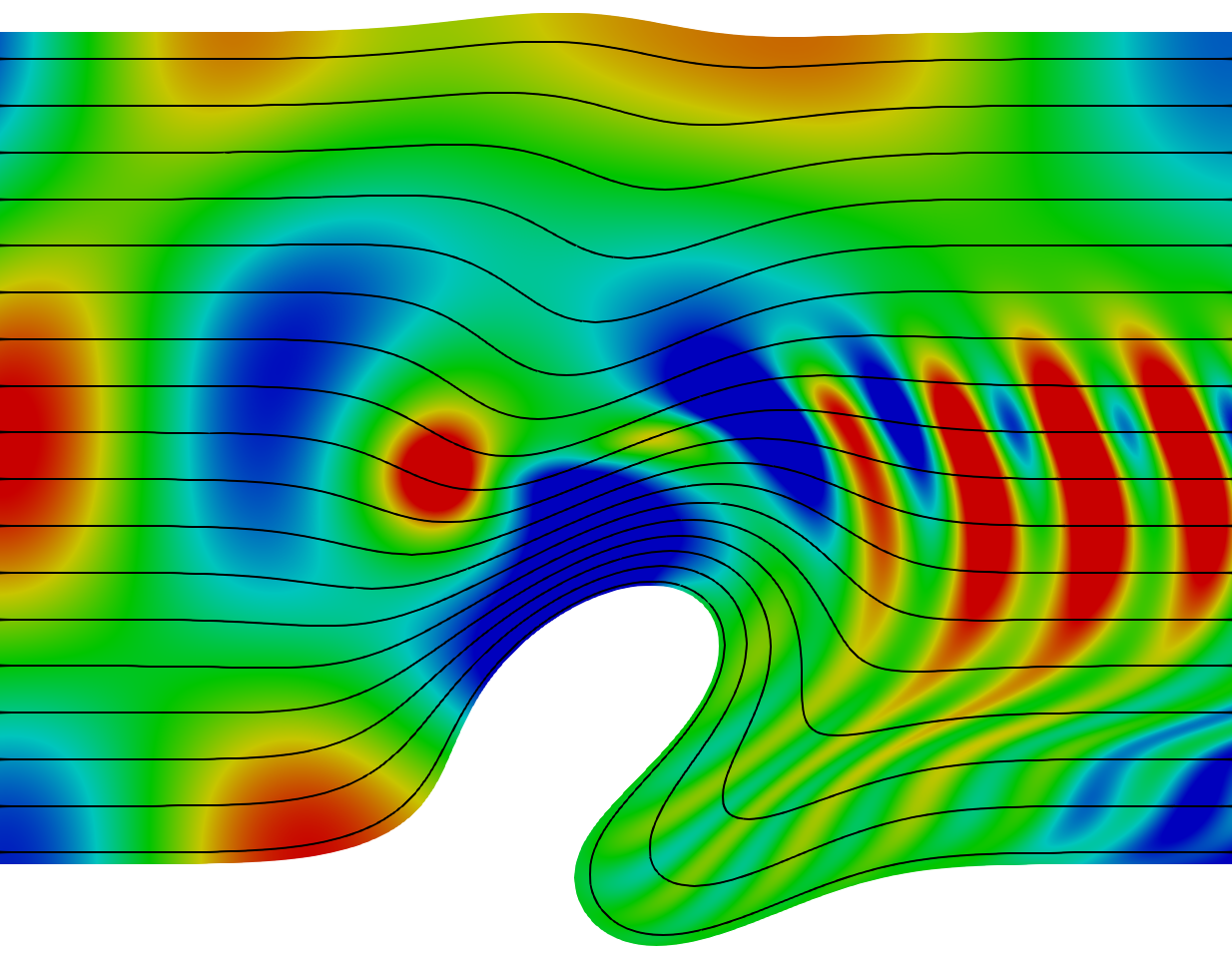
La simulation de la propagation acoustique harmonique en temps en présence d'un écoulement stationnaire (appelé écoulement moyen) est considérée. La difficulté est double car, aux difficultés habituelles de l'acoustique, s'ajoutent les difficultés liées aux phénomènes hydrodynamiques, induits par l'écoulement et couplés à l'acoustique. L'aéroacoustique est très proche des applications, principalement la réduction du bruit des avions et a donc fait l'objet d'une collaboration de longue date, initiée au début des années 2000, avec Airbus Group Innovations et plus récemment avec Naval Group.
Comme modèle pour l'aéroacoustique, plutôt que les équations d'Euler linéarisées, nous avons choisi les équations moins connues de Goldstein, mieux adaptées à notre avis à la fois à la théorie et au numérique. Les inconnues sont le potentiel des vitesses φ qui satisfait une équation de Helmholtz convectée et une inconnue hydrodynamique vectorielle ξ qui satisfait une équation de transport harmonique non classique. Les deux équations sont couplées.
L'analyse mathématique est basée :
(i) sur l'élimination de ξ, ce qui est possible pour des écoulements non résonnants qui correspondent à des écoulements sans recirculation ;
(ii) sur l'alternative de Fredholm pour le problème réduit en φ. On prouve que le problème est bien posé lorsque la vorticité φ de l'écoulement moyen est suffisamment faible.
En parallèle, nous avons considéré un écoulement simple, 1D et cisaillé. Nous avons alors pu développer un nouveau modèle dans lequel la description des phénomènes hydrodynamiques est simplifiée. Nous avons prouvé que ce modèle, initialement développé pour un écoulement moyen de faible nombre de Mach M, reste finalement très précis pour un nombre de mach modéré, associé à une faible erreur en M2.
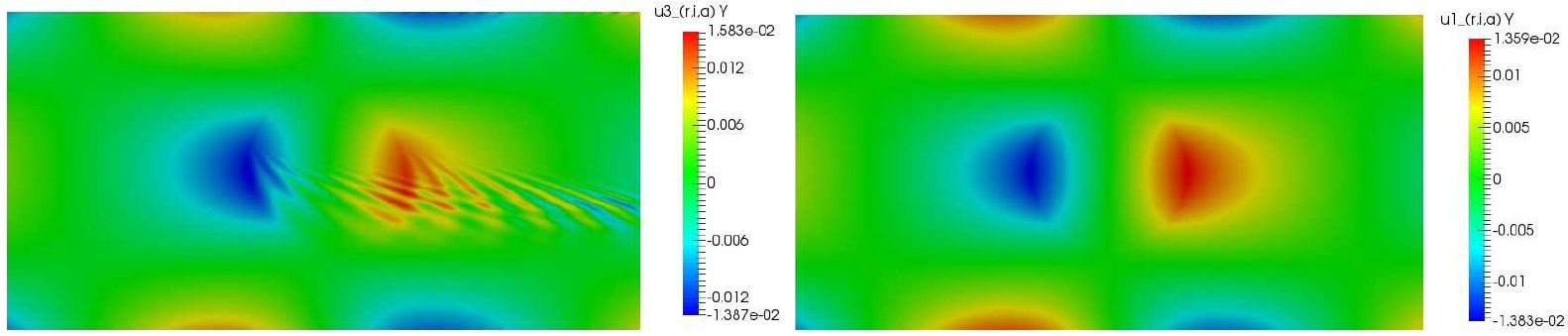
Couplage avec des ondes élastiques : résolution d'équations élastodynamiques linéaires à l'aide de potentiels
Il est difficile de simuler la propagation des ondes dans des milieux presque incompressibles tels que les tissus vivants mous car les ondes de cisaillement se propagent beaucoup plus lentement que les ondes de pression.
Le remède est l'utilisation de la décomposition de Helmholtz du champ de déplacement qui conduit au découplage des deux dynamiques, permettant de construire des discrétisations spatiales et temporelles adaptées à chaque type d'onde.
Mais alors l'enjeu est de traiter de manière stable les frontières et les interfaces, là où les deux ondes se recouplent, les approches directes conduisant à des instabilités sévères.
Nous avons construit, grâce à un cadre fonctionnel non standard, une formulation mixte stabilisée originale du problème, basée sur un choix judicieux de multiplicateurs de Lagrange vivant aux frontières et aux interfaces.



