Coupled phenomena for waves in fluids and solids

POEMS studies the acoustic propagation in complicated environments which couple phenomena propagating at very different speeds. A first example is the case of a moving fluid (aeroacoustics), in which acoustic waves and hydrodynamic waves (vorticity) propagate at very different speeds. A second example is given by an elastic solid, coupling naturally pressure and shear waves, which leads in the degenerated case of a nearly incompressible material to very different speeds of the two waves.

Aeroacoustics via Goldstein's equations

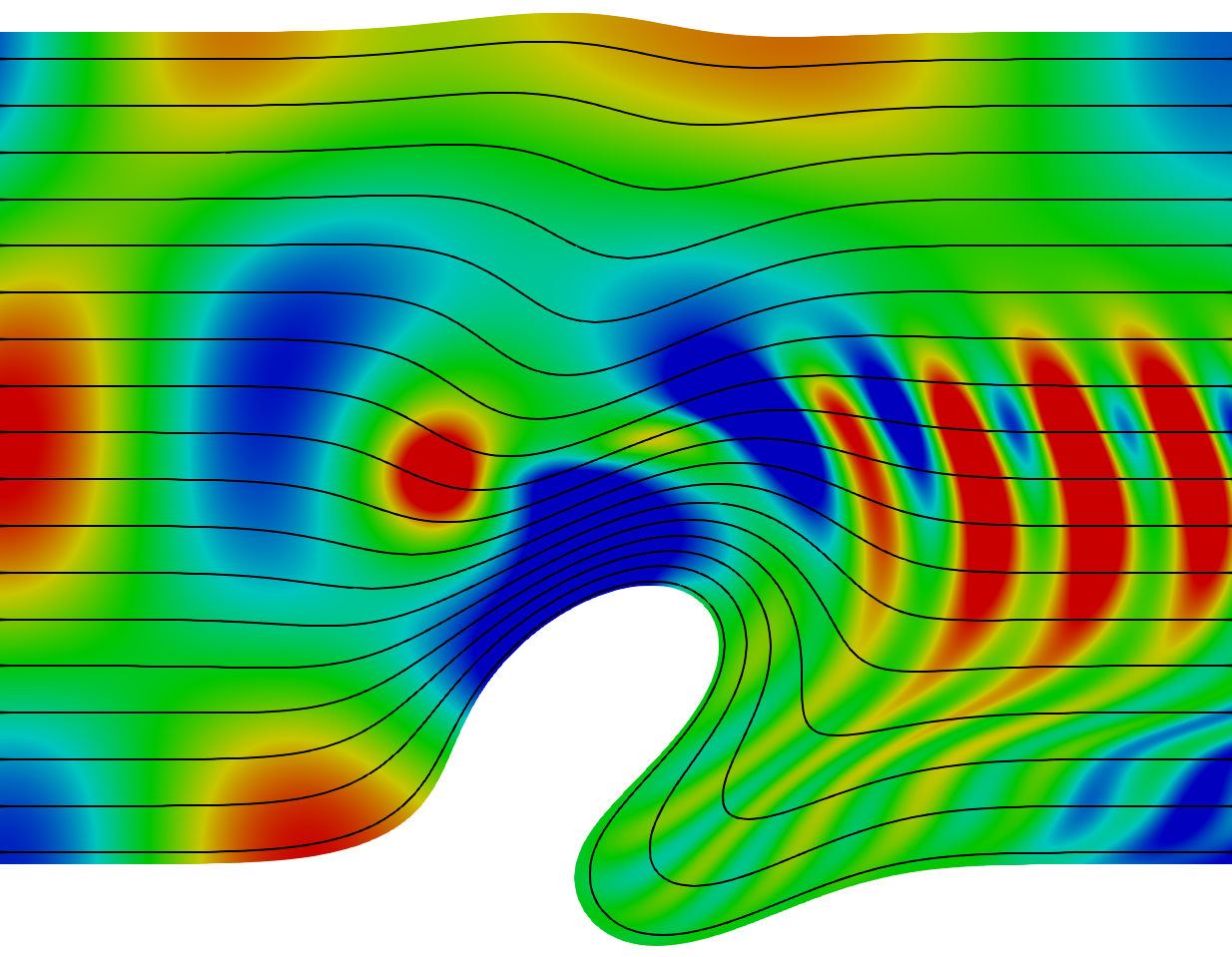
The simulation of time-harmonic acoustic propagation in presence of a stationary flow (called the mean flow) is considered. The difficulty is twofold because, in addition to the usual difficulties of acoustics, there are also difficulties arising from hydrodynamics phenomena, induced by the flow and coupled with the acoustic. Aeroacoustics is very close to applications, mainly the reduction of aircraft noise and therefore has been the object of a long term collaboration, beginning in the 2000's, with Airbus Group Innovations and more recently with Naval Group.

As a model for aeroacoustics, rather than the linearized Euler equations, we have chosen the less known Goldstein's equations, better suited in our opinion for both theory and numerics. The unknowns are the velocity potential φ which satisfies a convected Helmholtz equation and a vectorial hydrodynamic unknown ξ which satisfies a non-classical harmonic transport equation. Both equations are coupled.

The mathematical analysis is based:

(i) on the elimination of ξ, which is possible for non-resonant flows which correspond to flows without recirculation;

(ii) on the Fredholm's alternative for the reduced problem in φ. Well-posedness is obtained under a smallness assumption about the vorticity of the mean flow.

In parallel we have considered a simple 1D shear flow. We have then been able to develop a new model in which the description of hydrodynamic phenomena is simplified. We proved that this model, initially developed for a mean flow of low Mach number M, remains ultimately very precise for moderate Mach numbers, associated with a low error in M².

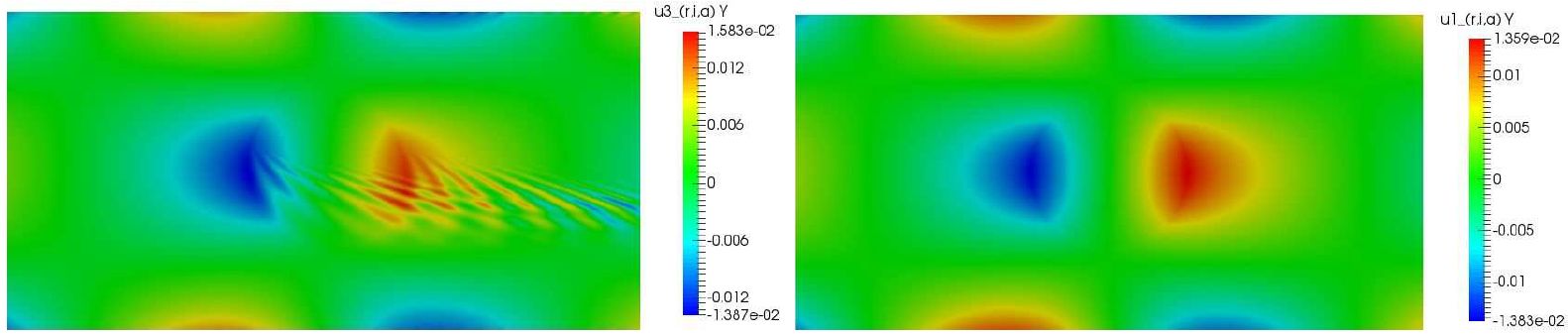
Coupling with elastic waves: solving linear elastodynamics equations using potentials

It is difficult to simulate the propagation of waves in nearly incompressible media such as soft living tissues because shear waves propagate much more slowly than pressure waves.

The remedy is to use the Helmholtz decomposition of the displacement field that leads to the decoupling of the two dynamics, allowing to build space and time discretizations adapted to each type of wave.

But then the challenge is to treat in a stable way boundaries and interfaces, where the two waves are recoupled, straightforward approaches leading to severe instability phenomena.

We built thanks to a non standard functional framework an original stabilized mixed formulation of the problem, based on a clever choice of Lagrange multipliers living on boundaries and interfaces.