Wave propagation in meta materials and dispersive media

This theme concerns propagative media whose physical features, which are usually represented by positive constants, become negative in some frequency ranges. This implies in particular that these media are dispersive, in the sense that their physical features depend on the frequency.

These materials can be natural, like metals and plasmas where the dielectric permittivity is almost real and negative in some frequency range. Besides, artificial metamaterials are build to achieve all possible strange properties: it is the case of negative index materials that have both a negative dielectric permittivity and a negative magnetic permeability at some frequencies, and of the hyperbolic metamaterials, which are anisotropic materials, with a non positive tensor permittivity.

All these materials give rise to unusual phenomena and possible physical applications are countless. In particular, negative index materials make physicists dream of spectacular devices like the perfect lens or the invisibility cloak.

The mathematical and numerical analysis of the related models, both in the time domain and the frequency domain, raises new open questions and challenges. For more than two decades, POEMS has greatly contributed to the understanding of these questions and the elaboration of adapted solutions: let us mention in particular the T-coercivity approach for sign-changing transmission problems and the Generalized Perfectly Matched Layers for negative index materials.

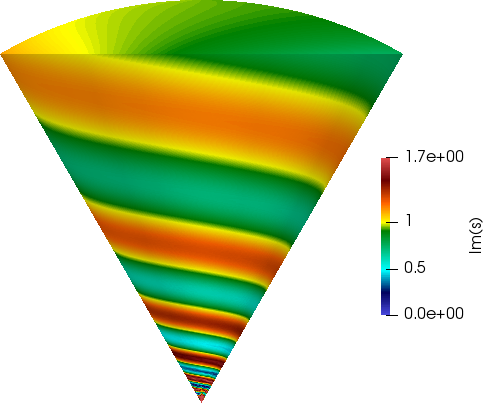
An important contribution of POEMS concerns the effect of corners at the boundary of a negative material, which give rise to a « black hole » phenomenon related to the behaviour of surface plasmons near corners. Most recent studies concern anisotropic materials for which the eigenvalues of the dielectric permittivity tensor are of opposite signs. They are called « hyperbolic », which reflects the fact that harmonic wave propagation is described by a hyperbolic rather than elliptic problem, a typical example being the Klein-Gordon equation.