Analyse asymptotique, homogénéisation et modèles effectifs

On considère dans ce travail des phénomènes décrits par les modèles usuels (essentiellement les équations de Helmholtz, de l'élasticité ou de Maxwell), la spécificité est la présence d'une couche mince, d'un revêtement mince, ou de coefficients oscillants, dont la dimension caractéristique est petite devant la longueur d'onde, ce qui pourrait rendre un calcul naïf prohibitif. Notre objectif est, en utilisant l'analyse asymptotique, de dériver des modèles efficaces, mieux adaptés au calcul analytique lorsque cela est possible et à la simulation numérique. Comme ces modèles effectifs ne sont qu'approximatifs, nous effectuons une analyse d'erreur, lorsque cela est possible, et illustrons numériquement la précision de ces modèles effectifs.

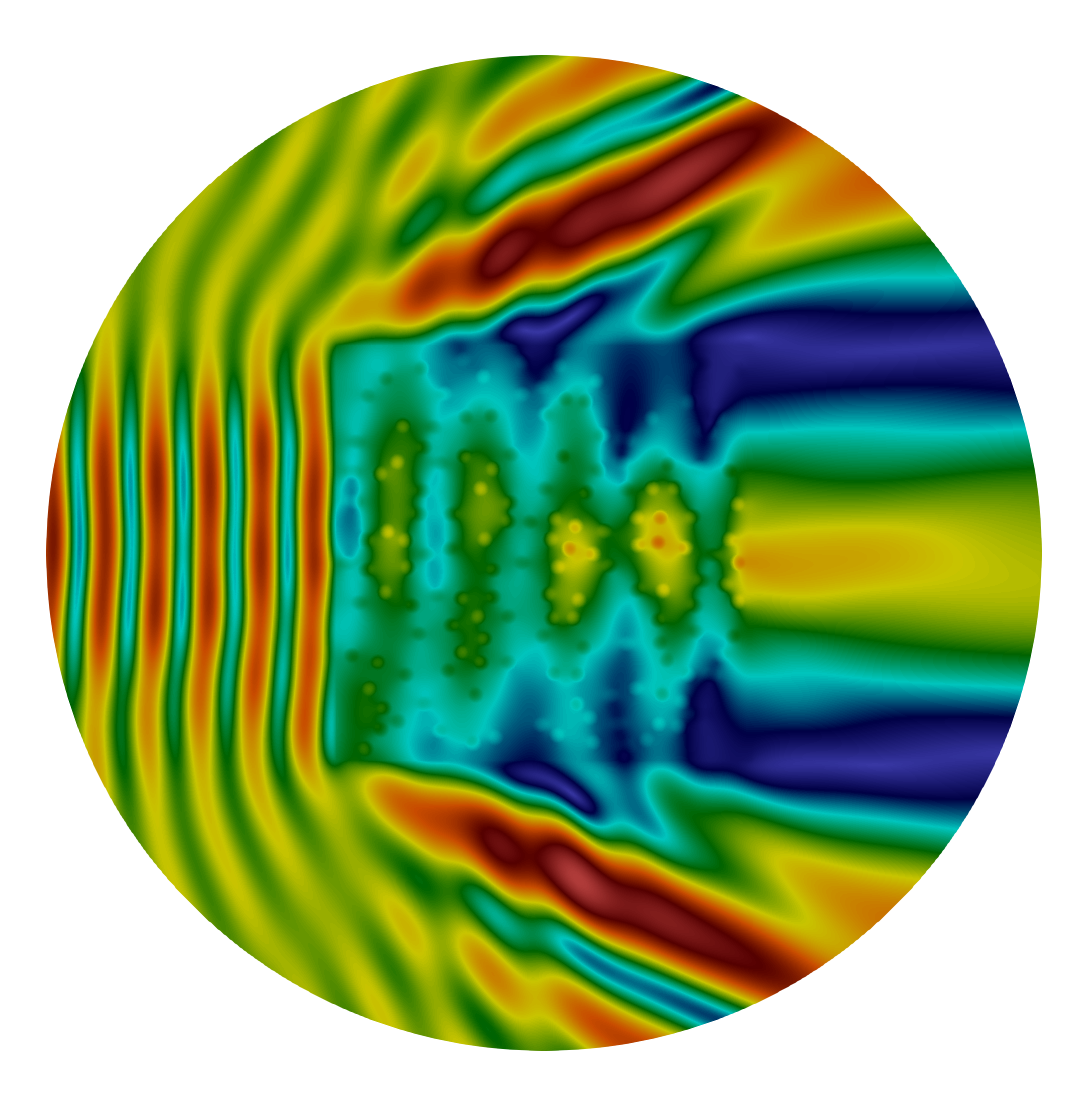
Conditions aux bords ou de transmission effectives en présence de couches ou de revêtement fins

Cette activité concerne la modélisation de couches ou de revêtements minces. A partir d'une analyse asymptotique par rapport à l'épaisseur de la couche, notée ε, on peut déduire des conditions effectives aux limites ou de transmission approchées. En remplaçant la couche par ces conditions, il n'est plus nécessaire de mailler la couche, ces conditions prenant en compte les phénomènes proches de la couche avec une erreur à certain ordre en ε. POEMS a développé une bonne expertise dans ce domaine ces dernières années. Plus récemment, nous avons adopté la même approche pour traiter des cas plus ambitieux : (1) des couches minces périodiques avec plusieurs micro-structures résonantes, (2) des couches minces aléatoires.

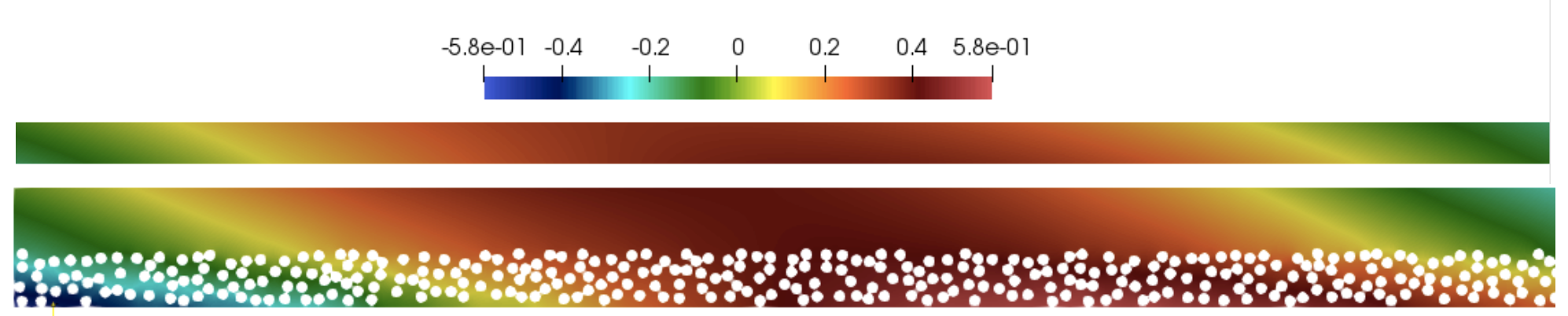
Homogénéisation périodique et aléatoire

Nous avons considéré dans ces travaux la propagation des ondes dans un milieu hétérogène dont la taille des hétérogénéités est petite devant la longueur d'onde. Le premier thème concerne la construction de modèles effectifs où le milieu hétérogène est remplacé par un milieu homogène équivalent. récemment, nous avons considéré deux situations. Dans le premier cas, le milieu est périodique avec des inclusions de matériaux négatifs. Dans le second cas, le milieu varie lentement (par rapport à la longueur d'onde) et contient de petites hétérogénéités réparties aléatoirement. Le deuxième thème est motivé par le fait que les modèles classiques homogénéisés sont bien adaptés aux milieux périodiques non bornés mais prennent mal en compte les phénomènes proches des interfaces ou des frontières. En utilisant un développement asymptotique enrichi, nous sommes en mesure de proposer des conditions aux limites effectives ou de transmission d'ordre élevé (similaire à celles obtenues en présence de couches minces).

Modèles de Foldy-Lax

Les modèles de Foldy-Lax sont des modèles asymptotiques utilisés pour calculer le champ diffracté par plusieurs petits obstacles. Alors que ces modèles sont assez bien étudiés dans le domaine fréquentiel, l'analyse en domaine temporel en est encore à ses balbutiements. Nous avons conçu un nouveau modèle de Foldy-Lax dans le domaine temporel à partir de la discrétisation de Galerkin d'un opérateur intégral de frontière à une seule couche et nous avons prouvé sa précision et sa stabilité.