Méthodes de décomposition de domaines

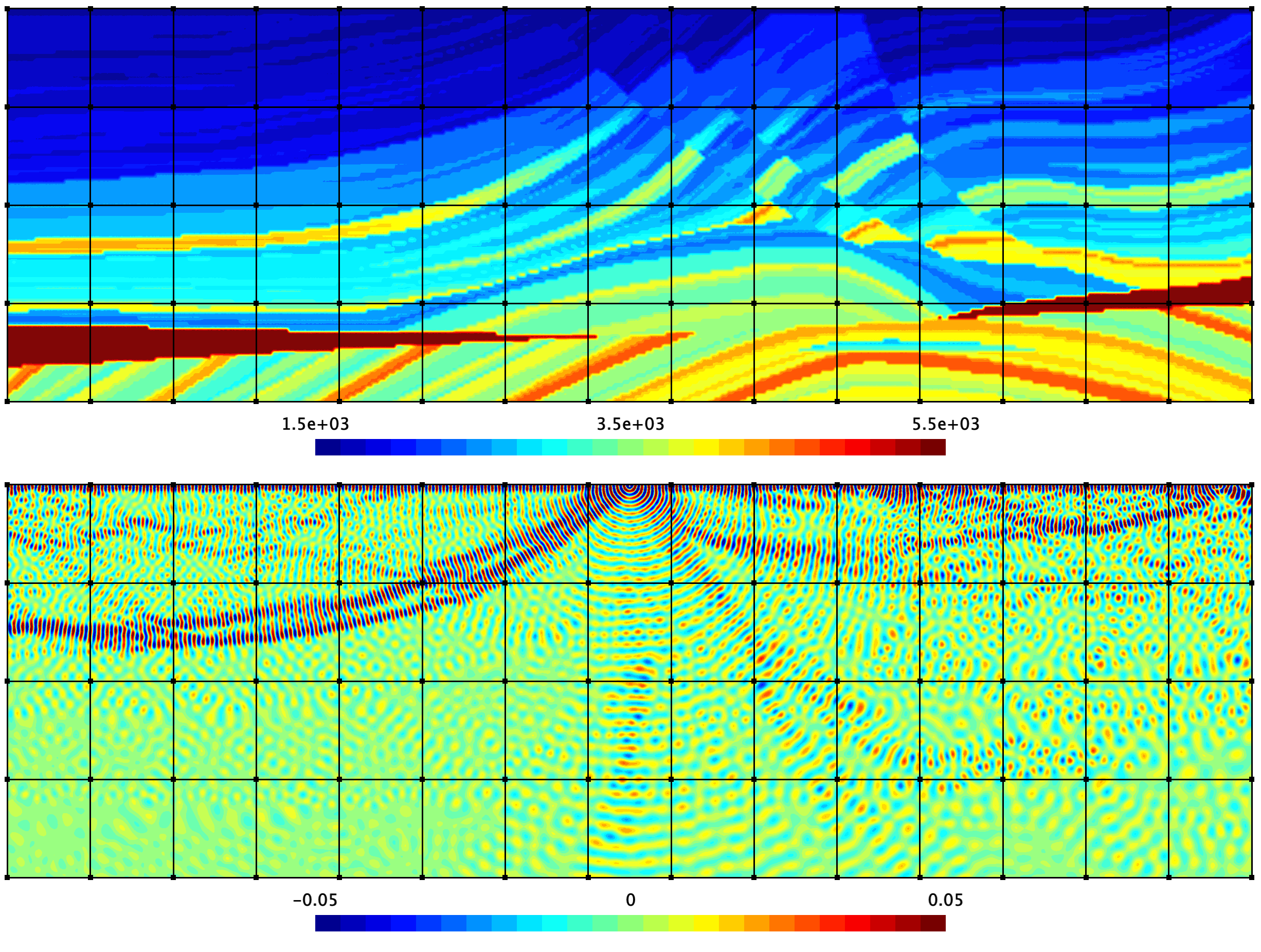
La recherche sur les méthodes de décomposition de domaine (DDM) est très active en raison du besoin en outils de simulation qui soient à la fois rapides et fiables. Ces méthodes permettent de traiter des problèmes de grande taille et de complexité croissante grâce à l’utilisation de calculateurs parallèles. Cependant, la conception de DDM efficaces et robustes pose des questions spécifiques non-triviales pour les problèmes de propagation d’ondes en régime harmonique. Les approches génériques développées pour les problèmes coercifs (ex. problèmes statiques) ne sont pas efficaces pour de tels problèmes.

Dans les années 1990, l’équipe POEMS a apporté plusieurs contributions importantes dans le développement et l’analyse mathématique de DDM pour les problèmes d’ondes en régime harmonique (PhD de B. Després et S. Ghanemi). Ce thème de recherche a fait un retour au sein de POEMS dans les années 2010, et fait maintenant partie des thèmes de prédilection de l’équipe.

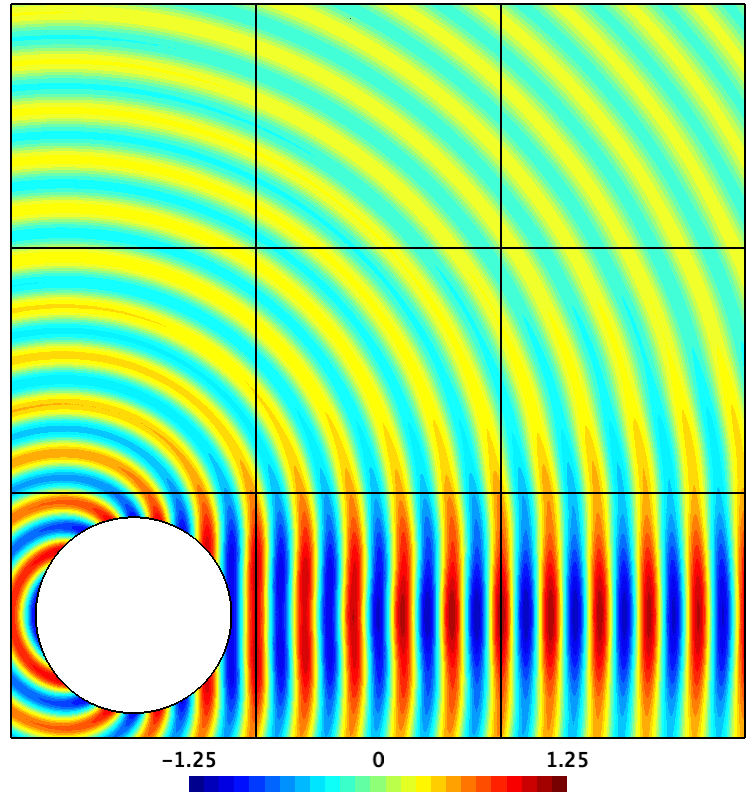
Plusieurs directions de recherche ont récemment été suivies. On peut citer le développement de DDM utilisant des conditions de transmission non-locales (permettant une convergence prouvée exponentielle) ou des conditions de transmission locales basées sur des techniques de frontière non-réfléchissante (ex. conditions absorbantes et PML). Cette direction de recherche s’appuie notamment sur l’expertise de l’équipe sur ces techniques. Des approches pour traiter des problèmes d’ondes électromagnétiques et des milieux anisotropies et complexes sont également à l’étude. Des recherches sur des DDM pour des problèmes physiques différents (ex. diffusion neutroniques) ont été motivées dans le cadre de collaborations industrielles.