Domain Decomposition Methods

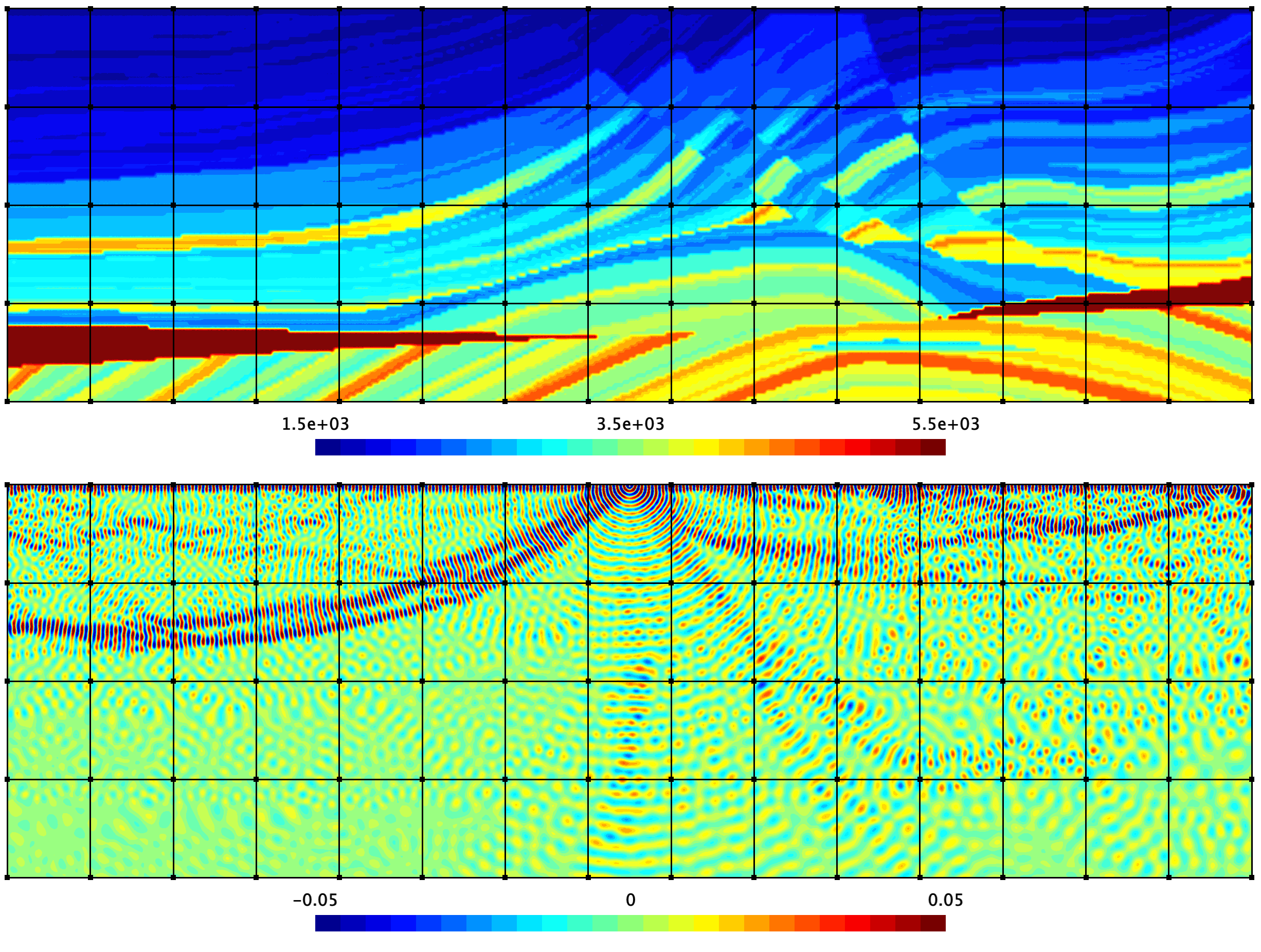
The research field of domain decomposition methods (DDM) is very active because of the critical need for numerical solvers that are reliable and computationally efficient. These methods are used to address problems of increasing size and increasing complexity thanks to the use of parallel computers. However, applying DDM to time-harmonic problems raises challenging questions, and generic approaches that are efficient for coercive problems (e.g., static problems) do not work for time-harmonic cases

In the 1990's, POEMS played a seminal role in the design and the analysis of DDM for time-harmonic wave propagation problems (PhD of B. Despres and S. Ghanemi). This research field made a comeback in the team in the 2010’s, and it is now a growing part of our activity, as devising efficient and robust solvers for wave propagation problems is one of our main goals.

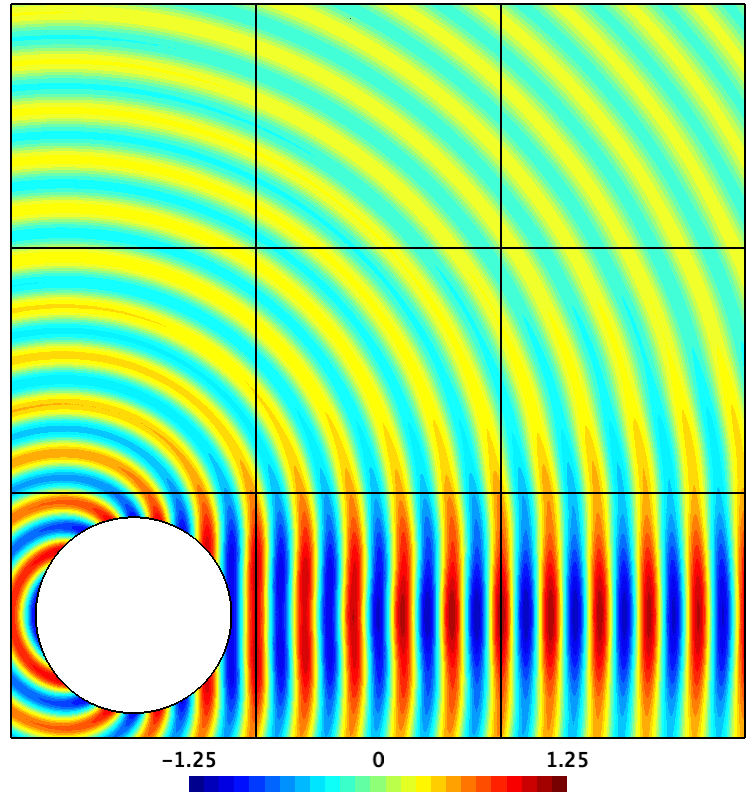
Several research directions have recently been followed. We can cite the development of DDM using non-local transmission conditions (providing proven exponential convergence) or local transmission conditions based on non-reflecting boundary techniques (e.g., absorbing boundary conditions and PML). This research direction relies in particular on the expertise of the team on non-reflecting techniques. Approaches to deal with electromagnetic problems and anisotropic/complex media are also being studied. Research on DDMs for different physical problems (e.g., neutron scattering) has been motivated by industrial collaborations.